Paper Notes: PeeK - Pruning for K-th Shortest Paths

Wang Feng, Shiyang Chen, Hang Liu, and Yuede Ji. PeeK: A Prune-Centric Approach for K Shortest Path Computation. International Conference for High Performance Computing, Networking, Storage, and Analysis, 2023. https://doi.org/10.1145/3581784.3607110

Observation

The solution of KSP (K Shortest Paths) problem is typically a small sub set of all available paths, even though the K is very large in a very large graph.

K Upper Bound Pruning

Based on the observation, the authors propose a prune-centric approach to KSP computation. The key idea is to prune the search space.

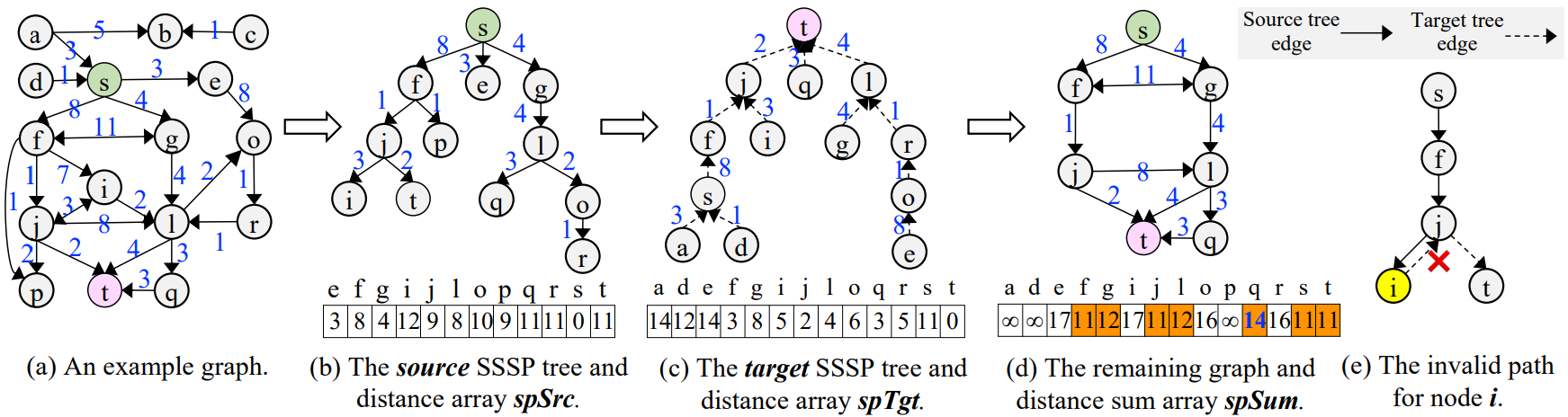
SSSP: Single Source Shortest Path

Start from the source node, get the shortest path to each node in the graph. Its result can basically represented as a tree, with the source node as the root. See figure (b).

Reverse SSSP:

Start from the target node, get the shortest path from each node in the directed graph. Its result can basically represented as a tree, with the target node as the root, but in opposite direction. See figure (c).

By combining the SSSP tree and the reverse SSSP tree, we can get all possible paths from the source to the target. It can be divided into two cases:

1. The vertices is not reachable from the source or to the target. For example, the vertex a can reach to the target t via a -> s -> f -> j -> t, but is not reachable from the source s.
   • The distance sum is basically denoted as infinity.
   • This is common for a sparse directed graph, as the observation above.
2. The vertices is reachable from the source and to the target. For example, the vertex o can reach to the target t via o -> r -> l -> t, and is reachable from the source s by s -> g -> l -> o.

Marked as reachable, this situation can be further divided into two parts. For example, the path obtained from o is s -> g -> l -> o -> r -> l -> t, and is can be clearly simplified as s -> g -> l -> t.

So the reachable paths are sorted by the distance sum, and only the top K paths are kept. The rest are pruned. For the illustration, the K = 3 and paths with distance sum 11, 12, 14 are kept as potential search space. See figure (d).

In actual implementation, vertices and edges that not presented in the first SSSP result can be pruned immediately, which helps to speed up the next SSSP computation.

This also applies to the second (reversed) SSSP, which can speed up the CSR format conversion.

CSR Representation of Sparse Graph

CSR (Compressed Sparse Row) is also used to represent the graph. The CSR representation is a common way to store a sparse matrix, whereas a graph can be viewed as an adjacency matrix.

Hand-on Experiment & Some Thoughts

I tried to run the provided code on my own machine, the testing script can be found at the appendix.

The testing script includes:

1. Graph generation with PaRMAT
2. Graph conversion to CSR format (make_csr)
3. Reachable pairs generation (make_reachable_src_dest)
4. Running the PeeK algorithm with different threads

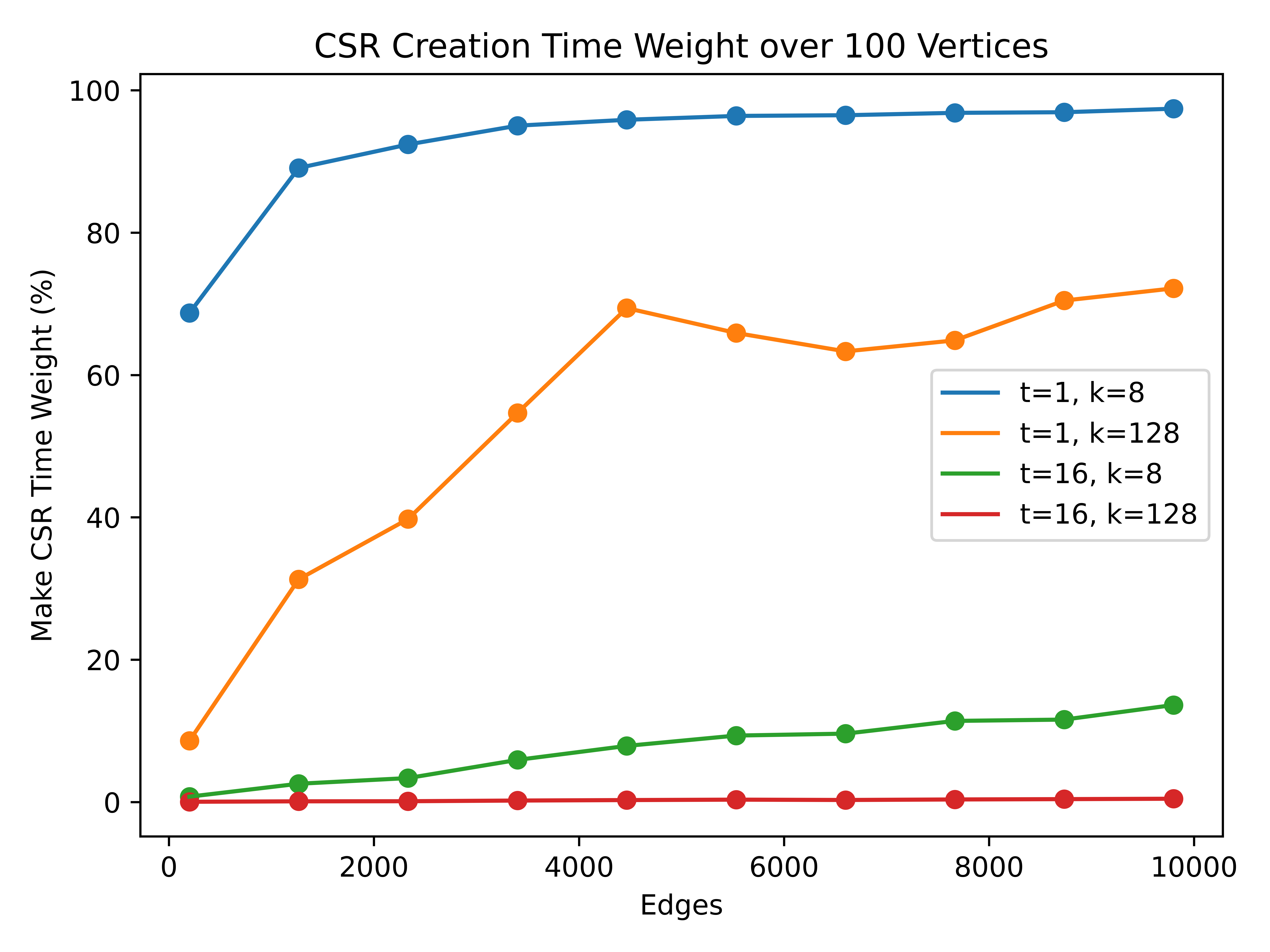
The above figure shows the percentage of the CSR conversion time over the total time. It is clear that, for a single threaded PeeK implementation, the CSR conversion time takes a significant part. Moreover, this part increases as the graph grows more dense. (Note that the fist point have sparsity rate of 97.98%, and the last point have 1.01%.) And actually, the running time of the PeeK algorithm is growing exponentially as the sparsity rate drops.

Understanding 1

The PeeK algorithm works better on a sparse graph. This also matches the behavior of K upper bound pruning – the more sparse the graph is, the more vertices and edges can be pruned.

Additionally, running make_csr would consume extreme large memory, and it can be observed that the memory consumption will grow to a peak and gradually decrease. For such memory-bound computation, memory size and access are also potential bottlenecks.

Understanding 2

The CSR conversion time is potentially a bottleneck for the PeeK algorithm. However, converting a graph to CSR format is also difficult to be parallelized.

For the multi-threaded PeeK implementation, CSR conversion time is relatively less weighted, which looks good. However, the running time is actually 50 to 300 times slower than the single threaded implementation. This is not expected, and I think it is due to the overhead of the multi-threading. Probably thread-wise communication and synchronization are the main reasons.

Understanding 3

The overhead of the multi-threading is not negligible for relatively smaller graph. The multi-threading is not always the best choice.

For the experiment and comparison section in the paper, it seems that the make_csr part is not counted in its running time. This is a potential issue, as the CSR representation of graph is significant for the PeeK algorithm, and its running time is not negligible.

Bug found

For a graph without enough paths to meet the K requirement, current implementation will fall into an infinite loop at make_reachable_src_dest. For example, a graph with 100 vertices and 100 edges, the PeeK algorithm try to meet K = 128 and loop forever.

Although the number of edges can not represent the number of possible paths, it still demonstrates the potential bug in the implementation.

Appendix

Source code of the testing script:

import subprocess
import numpy as np

LOG_FILE = "test.log"
MAX_VERTICES_NUM = 100000

MAKE_CSR_COMMAND = [
    "pwsh.exe",
    "-Command",
    "g++",
    "-O3",
    "-o",
    "make_csr.exe",
    "make_csr.cpp",
]

REACHABLE_COMMAND = [
    "pwsh.exe",
    "-Command",
    "g++",
    "-O3",
    "-I../includes",
    "-fopenmp",
    "-o",
    "make_reachable_src_dest.exe",
    "make_reachable_src_dest.cpp",
]


def get_max_edges_num(vertices_num: int) -> int:
    return vertices_num * (vertices_num - 1)


def calc_graph_sparsity(vertices_num: int, edges_num: int) -> float:
    return 1 - edges_num / get_max_edges_num(vertices_num)


def compile_util(command: list[str], cwd: str):
    """
    Compile a cpp file.
    """
    with open(LOG_FILE, "a") as f:
        f.write(f"@compile {command[-1]}\n")
        process = subprocess.run(
            command, shell=True, stdout=subprocess.PIPE, text=True, cwd=cwd
        )
        f.write(process.stdout)
        if process.returncode != 0:
            f.write(" ".join(command) + "\n")
            raise Exception(f"compile failed for {command[-1]}")


def gen_vertex_edge_pair(v: int, e: int) -> str:
    assert get_max_edges_num(v) >= e
    graph_file = f"./out/edge_list_v{v}_e{e}.txt"
    with open(LOG_FILE, "a") as f:
        f.write("================================\n")
        f.write(f"vertices: {v} \t edges: {e} -> {graph_file}\n")
        f.write(f"sparsity: {calc_graph_sparsity(vertices_num, e) * 100:.2f}%\n")
        f.write("@generate the graph (vertex edge pair)\n")
        command = [
            "pwsh.exe",
            "-Command",
            "./tools/PaRMAT/Release/PaRMAT.exe",
            "-nVertices",
            str(v),
            "-nEdges",
            str(e),
            "-a",
            "0.45",
            "-b",
            "0.22",
            "-c",
            "0.22",
            "-sorted",
            "-noEdgeToSelf",
            "-noDuplicateEdges",
            "-output",
            graph_file,
        ]
        process = subprocess.run(
            command, stdout=subprocess.PIPE, stderr=subprocess.PIPE, text=True
        )
        if process.returncode != 0:
            f.write(" ".join(command) + "\n")
            f.write(process.stdout)
            f.write(process.stderr)
            raise Exception(f"generate graph failed at v: {v}, e: {e}")
    return graph_file


def convert_graph_to_csr(graph_file: str) -> tuple[str, str, str]:
    prefix = graph_file.split(".")[1]
    begin_file = f".{prefix}.begin.bin"
    csr_file = f".{prefix}.csr.bin"
    val_file = f".{prefix}.val.bin"
    with open(LOG_FILE, "a") as f:
        f.write(f"@convert graph to csr\n")
        command = [
            "pwsh.exe",
            "-Command",
            "./tools/make_csr.exe",
            graph_file,
            begin_file,
            csr_file,
            val_file,
        ]
        process = subprocess.run(command, stdout=subprocess.PIPE, text=True)
        f.write(process.stdout)
        if process.returncode != 0:
            f.write(" ".join(command) + "\n")
            raise Exception(f"convert graph to csr failed at {graph_file}")
    return (begin_file, csr_file, val_file)


def gen_reachable_pairs(begin_file: str, csr_file: str, val_file: str) -> str:
    prefix = csr_file.split(".")[1]
    reachable_file = f".{prefix}.reachable.txt"
    with open(LOG_FILE, "a") as f:
        f.write(f"@gen reachable pairs\n")
        command = [
            "pwsh.exe",
            "-Command",
            "./tools/make_reachable_src_dest.exe",
            begin_file,
            csr_file,
            val_file,
        ]
        process = subprocess.run(
            command, stdout=subprocess.PIPE, stderr=subprocess.PIPE, text=True
        )
        with open(reachable_file, "w") as f2:
            f2.write(process.stdout)
        f.write(process.stderr)
        if process.returncode != 0:
            f.write(" ".join(command) + "\n")
            raise Exception(f"gen reachable pairs failed at {reachable_file}")
    return reachable_file


def run_peek_with_threads(
    begin_file: str, csr_file: str, val_file: str, reachable_file: str, threads: int
):
    with open(LOG_FILE, "a") as f:
        f.write(f"@run peek with threads: {threads}\n")
        command = [
            "pwsh.exe",
            "-Command",
            f"./peek_adaptive_with_status_array_kbound_thread_{threads}.exe",
            begin_file,
            csr_file,
            val_file,
            reachable_file,
        ]
        process = subprocess.run(
            command, stdout=subprocess.PIPE, stderr=subprocess.PIPE, text=True
        )
        f.write(process.stdout)
        if process.returncode != 0:
            f.write(" ".join(command) + "\n")
            f.write(process.stderr)
            raise Exception(
                f"run peek failed at {reachable_file} with {threads} threads"
            )


if __name__ == "__main__":
    with open(LOG_FILE, "w") as f:
        f.write("test start\n")

    # compile_make_csr()
    # compile_make_reachable_src_dest()
    compile_util(MAKE_CSR_COMMAND, "./tools")
    compile_util(REACHABLE_COMMAND, "./tools")

    vertices_num = 100
    while vertices_num <= MAX_VERTICES_NUM:
        max_edges_num = get_max_edges_num(vertices_num)
        print(f"{vertices_num}, {max_edges_num}")
        for edges_num in np.linspace(vertices_num * 2, max_edges_num - vertices_num, 10):
            edges_num = int(edges_num)
            print(f"\t{vertices_num}, {edges_num}")
            graph_file = gen_vertex_edge_pair(vertices_num, edges_num)
            begin_file, csr_file, val_file = convert_graph_to_csr(graph_file)
            reachable_file = gen_reachable_pairs(begin_file, csr_file, val_file)
            run_peek_with_threads(begin_file, csr_file, val_file, reachable_file, 1)
            run_peek_with_threads(begin_file, csr_file, val_file, reachable_file, 16)

        vertices_num *= 10