Paper Notes: Dynamic Inference of Convolutional Neural Networks

Wenhan Xia, Hongxu Yin, Xiaoliang Dai and Niraj Kumar Jha. Fully Dynamic Inference With Deep Neural Networks. IEEE Transactions on Emerging Topics in Computing, 2020. https://doi.org/10.1109/TETC.2021.3056031

Observation

CNN layers and features have heavy input-dependence, which can be exploited to reduce (i.e., be ignored) the computational cost of inference.

Thus, only salient layers for current input (which was decided by Layer Net, L-Net) are computed, while others are skipped. This also applies to the feature maps/ channels (which was decided by Channel Net, C-Net) within a layer.

Design

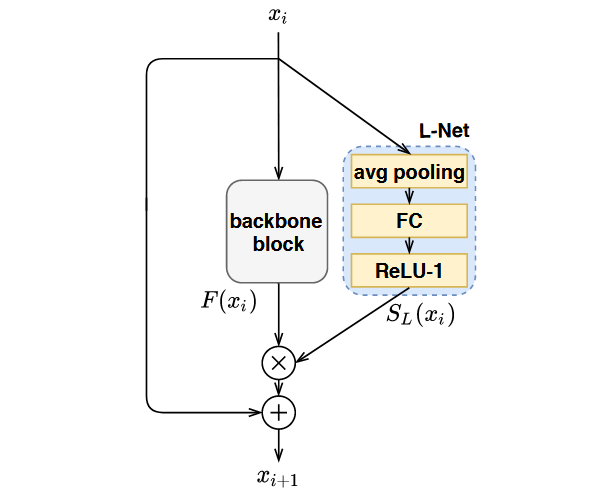
L-Net

The L-Net is inspired by the concept of block-based residual learning.

▶

Side Note on Block-Based Learning (Click here to unfold/fold)

Side Note on Block-Based Learning

Introduced by He et al. in Deep Residual Learning for Image Recognition, the block-based residual learning is a technique to improve the training of convolutional neural networks. The core idea is to add the output of a block with the input (i.e., residual), which is then passed through a non-linear activation function. This enables the network to grow deeper without the vanishing gradient problem.

For example, ResNet in PyTorch is constructed by several blocks.

from torchvision.models import resnet18

model = resnet18()
# print(model._modules)
print(model._modules['layer1'])

The output would be like:

Sequential(
  (0): BasicBlock(
    (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (relu): ReLU(inplace=True)
    (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  )
  (1): BasicBlock(
    (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (relu): ReLU(inplace=True)
    (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  )
)

The generated resnet18 has 4 main layers (besides some initial layers and fully connected layers afterwards), each of which are constructed by two blocks BasicBlock. The BasicBlock is where the residual adding is performed.

Let’s see its forward() function:

class BasicBlock(nn.Module):
    def forward(self, x: Tensor) -> Tensor:
        identity = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        if self.downsample is not None:
            identity = self.downsample(x)

        out += identity
        out = self.relu(out)

        return out

Note the out += identity line, which is the key to the residual learning. (Downsampling is simply a technique to match the dimensions of identity and out.)

For ResNet 50 and above, the BasicBlock is replaced by Bottleneck block, which contains different structure of conv layers, but the residual learning is the same.

Jump back to the main content.

It mainly have 3 components:

1. a global average pooling layer over the input feature map;
2. a fully connected layer;
3. a ReLU-1 activation function.

The output of L-Net layer would be the block salience score, ranging from 0 to 1. The higher the score, the more salient the block is. This score is applied to the block output as a scaling factor, and if the score is 9, meaning that the block is skipped.

The philosophy is to design the additional layers to be lightweight, so that no significant overhead is introduced.

The L-Net would be attached to each block in parallel.

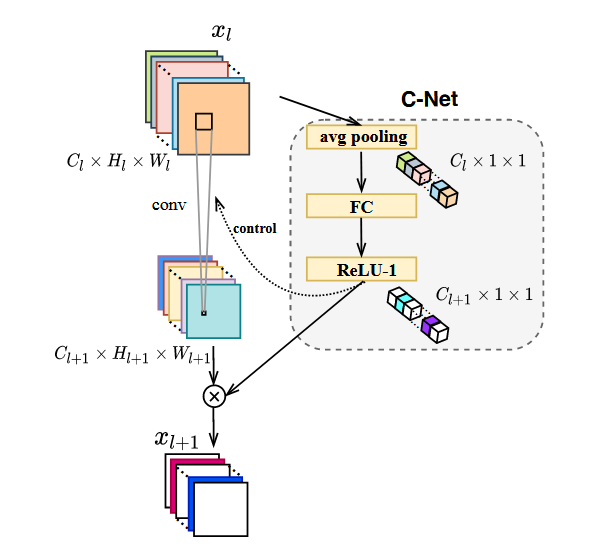
C-Net

Similarly for the convolutional computation inside each block, a convolutional layer may also be skipped if it is not salient for the current input. Thus, the C-Net is exactly the same as L-Net, except that

1. Different location in the network, i.e., attached to each convolutional layer in parallel;
2. Different size of the net, i.e., the input size is the feature map of the convolutional layer, and the output size is a 1D vector of length equal to the number of channels in the feature map.

LC-Net

The actual implementation is a combination of L-Net and C-Net, which is called LC-Net. This is because part of L-Net and C-Net can be shared, such as the global average pooling layer at the beginning.